To the Moon - insomnihack 2024 teaser

Feb 04, 2024

This is a write-up of the crypto-ctf challenge ‘To The Moon’ from insomnihack 2024 teaser. I worked on this with my teammate P3taByte.

Challenge Handout

We are given a r1cs-file which somehow encodes the flag.

File: flag_constraints-c4328e47faf6ab5667ee70ac2f1e7225324f519aec5a525ad29de428432dcb17.r1cs

0000000000000000: 7231 6373 0100 0000 0300 0000 0200 0000   r1cs............
0000000000000010: 7800 0000 0000 0000 0100 0000 0100 0000   x...............
0000000000000020: 0000 00f0 93f5 e143 9170 b979 48e8 3328   .......C.p.yH.3(
0000000000000030: 5d58 8181 b645 50b8 29a0 31e1 724e 6430   ]X...EP.).1.rNd0
0000000000000040: 0100 0000 0100 0000 0100 0000 0000 0000   ................
0000000000000050: 0000 0000 0000 0000 0000 0000 0000 0000   ................
0000000000000060: 0000 0000 0000 0000 0100 0000 0000 0000   ................
0000000000000070: 9a68 0fb9 8788 1640 cb76 94e8 2a88 3103   [email protected]..*.1.
0000000000000080: b7a0 a7d7 cf11 bb95 8daa 58f0 27c4 4410   ..........X.'.D.
0000000000000090: 0100 0000 4000 0000 0000 0000 2000 0000   ....@....... ...
00000000000000a0: 0100 00f0 93f5 e143 9170 b979 48e8 3328   .......C.p.yH.3(
00000000000000b0: 5d58 8181 b645 50b8 29a0 31e1 724e 6430   ]X...EP.).1.rNd0
00000000000000c0: 0200 0000 0000 0000 0100 0000 0000 0000   ................
00000000000000d0: 0200 0000 0000 0000 0100 0000 0300 0000   ................
00000000000000e0: 1000 0000 0000 0000 0000 0000 0000 0000   ................
00000000000000f0: 0100 0000 0000 0000                       ........

Some Preliminaries

r1cs find their use in Non-interactive zero-knowledge proofs.

What are zero-knowledge proofs.

Please keep in mind that this written from the perspective from a zk-noob. That means you are legally obliged to report any inaccuracies to me!

Non-interactive zero-knowledge proofs find widespread use in the cryptography/cryptocurrency world. Their basic premise is that a ‘prover’ is trying to proof knowledge of a factoid to an outside party, the verifier, without leaking any information about the factoid.

How is this seemingly-paradoxical feat accomplished in practice?

Lots of black-magic moon math, that is better explained elsewhere.

Why zksnarks, What?

zk-snarks are zero-knowledge proofs satisfying special properties. zk-snarks in turn find their use in the crypto(currency) world.

The r1cs format finds its use in the pipeline for building zk-snarks.

Why Circuits, What?

Q: What exactly does the prover want to convince the verifier of?

A: The zk-people use circuits to express the statements that the prover will prove to the verifier.

It makes sense to use circuits because they are very powerful and you can express a lot of problems with them.

Why Polynomials, What?

zk-snarks encode the computation that prover wants to prove to the verifier in an arithmetic circuit. Arithmetic circuits are basically just circuits that evaluate polynomials.

What is r1cs?

Now it is time to define the r1cs. Short for Rank-1 Constraint System (r1cs).

🚨 All math operations are done module a prime p, unless stated otherwise

For an r1cs we need:

coefficient vectors $a, b, c$ in some prime field
vector of unknowns $x$

This is the system of constraints:

\langle a, x \rangle \langle b, x \rangle = \langle c, x \rangle

that people call r1cs.

The challenge

The file flag_constraints-c4328e47faf6ab5667ee70ac2f1e7225324f519aec5a525ad29de428432dcb17.r1cs comes in the r1cs format which is understood by the snarkjs tool. Let’s inspect it.

The format

louis@bounce:~/insomni/moon$ snarkjs r1cs export json flag_constraints-c4328e47faf6ab5667ee70ac2f1e7225324f519aec5a525ad29de428432dcb17.r1cs lmao.json
[INFO]  snarkJS: undefined: Loading constraints: 0/1
[INFO]  snarkJS: undefined: Loading map: 0/2
louis@bounce:~/insomni/moon$ cat lmao.json 
{
 "n8": 32,
 "prime": "21888242871839275222246405745257275088548364400416034343698204186575808495617",
 "nVars": 2,
 "nOutputs": 0,
 "nPubInputs": 1,
 "nPrvInputs": 0,
 "nLabels": 2,
 "nConstraints": 1,
 "useCustomGates": false,
 "constraints": [
  [
   {
    "1": "21888242871839275222246405745257275088548364400416034343698204186575808495616"
   },
   {
    "1": "1"
   },
   {
    "0": "7358504996770508486687187130827958137520805565857056985433965719766776637594"
   }
  ]
 ],
 "map": [
  0,
  1
 ],
 "customGates": [
 ],
 "customGatesUses": [
 ]

The filename of the handout already hints at the flag being hidden in the constraints. Let’s take a closer look. First we need to understand how polynomials (arithmetic) circuits are converted to constraints.

How exactly do I encode a polynomial into a r1cs?

We are going to start with a polynomial (arithmetic circuit) and then convert it into arithmetic circuit. Let’s say we want to encode the following constraint:

x^{2} - 16 = 0

We will begin by flattening this expression. How do you do that? Here also visualised as a tree:

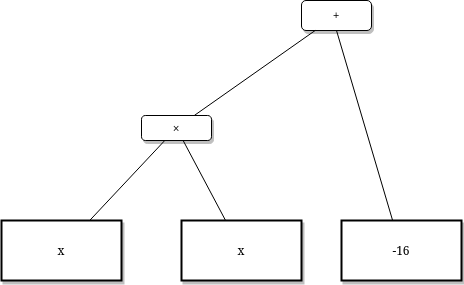
First step is to flatten the polynomial expression. By flatten we mean: Introduce new variables such that the original polynomial equation can be written as formulaes of the form

a = b \text{ op } c

x = y

which in our example boils down to

x_2 = x_1 * x_1

x_3 = x_2 - 16

The individual flattend operations are called gates! We now have four different variables $x =(x_0, x_1, x_2, x_3)$ and two gates.

🚨 We explicitely set

x_0 = 1

, else we would not be able to express adding/subtracting constants in a R1Cs

Each of these gates we will turn into a R1CS. That means 2 R1CS where the vectors $a$ , $b$ , $c$ and $x$ are 4-dimensional. Remember in R1CS:

\langle a, x \rangle \langle b, x \rangle = \langle c, x \rangle

Let’s figure out what values $a$ , $b$ and $c$ take on.

Gate	Value of $a$	Value of $b$	Value of $c$
$x_2 = x_1 * x_1$	$(0, 1, 0, 0)$	$(0, 1, 0, 0)$	$(0, 0, 1, 0)$
$x_3 = x_2 - 16$	$(0, 0, 1, 0)$	$(-16, 0, 0, 0)$	$(0, 0, 0, 1)$

We did it! This format can now be used for further processing in the zk-snark pipeline. Next steps would be to turn this into a QAP (Quadratic Arithmetic Program). You can read more on that in this blogpost by Vitalik Buterin: Quadratic Arithmetic Programs: from Zero to Hero

Solving that challenge

Recall that in the challenge we get a r1cs

{
 "n8": 32,
 "prime": "21888242871839275222246405745257275088548364400416034343698204186575808495617",
 "nVars": 2,
 "nOutputs": 0,
 "nPubInputs": 1,
 "nPrvInputs": 0,
 "nLabels": 2,
 "nConstraints": 1,
 "useCustomGates": false,
 "constraints": [
  [
   {
    "1": "21888242871839275222246405745257275088548364400416034343698204186575808495616"
   },
   {
    "1": "1"
   },
   {
    "0": "7358504996770508486687187130827958137520805565857056985433965719766776637594"
   }
  ]
 ],
 "map": [
  0,
  1
 ],
 "customGates": [
 ],
 "customGatesUses": [
 ]

Let’s look at the constraints more closely:

 "constraints": [
  [
   {
    "1": "21888242871839275222246405745257275088548364400416034343698204186575808495616"
   },
   {
    "1": "1"
   },
   {
    "0": "7358504996770508486687187130827958137520805565857056985433965719766776637594"
   }
  ]
],

This encodes the constraint:

- x_{1}^{2} + 7358504996770508486687187130827958137520805565857056985433965719766776637594 x_0 = 0

We mostly figured this out by guessing/experimenting with constraints of small example circuits I wrote in circom

Again $x_0 = 1$ because elsewise you can not add/subtract constants. With $x_0 = 1$ this is a constraint, we can easily solve in sage:

F = GF(21888242871839275222246405745257275088548364400416034343698204186575808495617);

R.<x> = PolynomialRing(F);
(- x * x - 7358504996770508486687187130827958137520805565857056985433965719766776637594).roots();

convert both root’s bytes to ascii and observe flag in one of them. Flag is b'INS{Nothing_to_hide_in_R1CS!!!}'